
a) Author to whom correspondence should be addressed: Group for Ferroelectrics and Functional Oxides, Swiss Federal Institute of Technology in Lausanne –ĞPFL,đ015 Lausanne, Switzerland Electronic Materials Research Laboratory, Key Laboratory of the Ministry ofĞducation & International Center for Dielectric Research, School of Electronic and InformationĞngineering, Xi’an Jiaotong University, Xi’anė10049,Ĝhina Electronic Ceramics Department, Jožef Stefan Institute, Jamova Cesta 39, 1000, Ljubljana, Slovenia Riemer, Li Jin, Hana Uršič, Mojca Otonicar, Tadej Rojac, andĝraganĝamjanovic. An experimental approach based on a lock-in technique that is well-suited for such studies is also discussed.ġ1 Dielectric and electro-mechanic nonlinearities in perovskite oxide ferroelectrics, relaxors and relaxor ferroelectrics

We review the basic formalism of the nonlinear description of polarization and strain, give a physical interpretation of different terms and illustrate this approach on numerous examples of relaxors, relaxor ferroelectrics, hard and soft ferroelectrics, and morphotropic phase boundary compositions. In this paper we show that an investigation of nonlinear behavior is a sensitive way to study various mechanisms operating in dielectric and piezoelectric materials. Most ferroelectrics exhibit nonlinear response at all practical field levels meaning that the apparent material coefficients depend on the amplitude of the driving excitation.
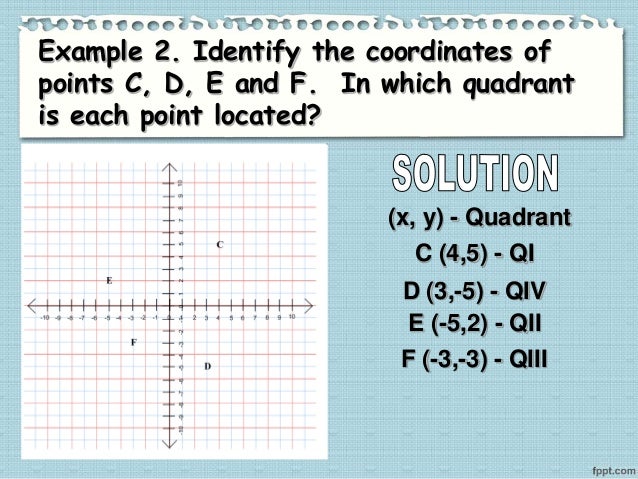
One signature of these processes is nonlinearity of the strain and polarization. Examples include motion of ferroelectric and ferroelastic domains, presence of domains within domains, dynamics of different types of polar nano-entities, interaction of polar nano-entities (e.g., polar nanoregions in relaxors) with the strain and polarization within domains, motion of defects and rearrangement of defect clusters and their interaction with polarization and strain. The reason for this is that many processes in a ferroelectric material contribute to its properties, often concurrently. The response of real ferroelectric and related materials is in general complex and difficult to interpret. The center of the Cartesian grid, the intersection point of the axes, is called the origin of the graph.Īny point in the Cartesian plane can be located by specifying its two coordinates, x and y.The polarization and strain response of ferroelectric materials at fields below the macroscopic coercive field is of a paramount importance for the operation of many electronic devices. If each axis is like a 1-dimensional number line, where x is positive on the right, negative on the left, and y is positive above the x-axis and negative below it, we have these results for each quadrant: Quadrant The two axes divide the Cartesian plane into four quadrants, which we label, beginning with the upper right and moving around counterclockwise, as Quadrants I, II, III and IV, using Roman numerals. We don't usually use "ordinate" and "abscissa" too much these days, but you should know that you might hear them.

The horizontal axis is called the abscissa and is usually labeled as the x-axis. The vertical axis is called the ordinate, and is usually labeled as the y-axis. The Cartesian coordinate system consists of two axes (plural of axis) drawn at right angles to one-another.


 0 kommentar(er)
0 kommentar(er)
